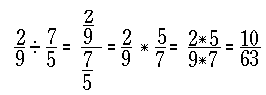Nachfolgend werden die
wesentlichen Zusammenhänge der Bruchrechnung angeführt. Der Bruchstrich
ist nichts anderes als ein Geteiltzeichen. Es gilt:
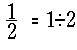
Hat ein Bruch im Zähler
und Nenner gleiche Faktoren, so können diese gekürzt werden:
![]()
Da der Faktor 5 sowohl im Zähler als auch im Nenner auftaucht, können jeweils Zähler und Nenner durch diesen Faktor gekürzt werden.
Beim Kürzen steht zwischen den Ausdrücken ein Gleichheitszeichen; somit gilt die Regel des Kürzens auch "rückwärts". Brüche können also im Zähler und Nenner gleichzeitig mit beliebigen Faktoren multipliziert werden. Dieses Verfahren nennt man Erweitern des Bruches.
![]()
Zwei Brüche werden
multipliziert, indem jeweils die Zähler und die Nen-
ner miteinander multipliziert
werden:
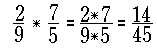
Dividiert (geteilt) werden Brüche, indem mit dem Kehrwert multipliziert wird:
![]()
Auch, wenn Brüche dividiert werden, kann natürlich das "Geteilt-Zeichen" durch einen Bruchstrich ersetzt werden: